Binary Calculator

About Our Binary Converter

Welcome to use our binary number calculator. Read this article to explore the fascinating world of binary numbers and delve into the operations of a binary calculator. No matter what, whether you are a computer science enthusiast or a curious fellow about binary arithmetic, this will enlighten you with all the information you are looking for to understand the use of a binary calculator effectively.

What is a Binary Number?

A binary number is a set of numerical systems that counts on only two symbols: 0 and 1. It's unlike a decimal system in which the base is 10 and has ten digits from 0-9. The binary system works on the base-2 system. Each digit in a binary number is considered a "bit," which represents a power of 2.

• The rightmost bit contains the value of (two's power zero) 2^0, that is 1,
• The next bit to the left contains the value of (two's power one) 2^1 that is 2,
• Then 2^2 (two's power 2), that is 4, and so on.

Binary numbers are highly utilized in digital systems and computers as they offer a simple and efficient way of representing and manipulating data using electronic circuits. Binary numbers have formed the foundation of modern digital technology.

How Does the Binary Calculator Work?

The easiest calculator to use, you can say, is a binary calculator. This tool enables you to carry out various arithmetic operations on binary numbers. It works just like a regular calculator but will use the binary system rather than the decimal one. The binary calculator will automatically understand the binary notation and work on subtraction, addition, multiplication, and division operations accordingly.

We present a user-friendly interface binary calculator that will make your calculations easy and hand you accurate results for all your binary arithmetic needs. Try it now!

How to Use the Binary Calculator?

It is quite easy to operate a binary calculator. Follow the step-by-step process to use it effectively.

• Click here to use the binary calculator.
• Put the binary numbers you want to perform calculations on.
• Make sure the numbers contain only 0 and 1.
• Choose the desired operations from (+,-,*,/)
• Lastly, click on 'calculate' to get the accurate results.

Now let's dive into the process of converting binary to decimal and decimal to binary numbers.

1. Binary to Decimal:

Switching from binary to decimal is important to understand binary arithmetic in our routine decimal system.

• First, write down the binary number.
• Assign powers of 2 to each bit from right to left (from 2^0, 2^1, 2^2, and so on).
• Now, multiply each bit by its corresponding power of 2.
• Lastly, add up the results to obtain the decimal equivalent.

Look at the example converting the binary number 1011 to decimal:

1 x 2^3 = 8

0 x 2^2 = 0

1 x 2^1 = 2

1x 2^0 = 1

8 + 0 + 2 + 1 = 11

Also, you can use binary to a decimal calculator or binary to decimal converter for quick results.

2. Decimal to Binary:

Switching a decimal number to binary allows us to represent numbers using the binary system. Follow each step to convert decimal to binary:

• Divide the chosen decimal number by 2 and write down the remainder.
• Repeat dividing the quotient by 2 until the quotient becomes 0.
• Jot down the remainder in reverse order to get the binary equivalent.

Look at the example converting the decimal number 11 to binary.

11/2 = 5 with a remainder 1

5/2 = 2 with the remainder 1

2/2 = 1 with remainder 0

½ = 0 with remainder 1

Now write the remainder in reverse order, i.e., 1011.

You can perform a quick and accurate calculation using a decimal to binary calculator or a decimal to binary converter.

How Should We Add, Subtract, Multiply & Divide Binary Numbers?

Binary addition, subtraction, multiplication, and division are important operations in binary arithmetic. A binary calculator makes the calculations easiest. Have a look at a brief overview of each operation.

Binary Addition:

If you want to add two binary numbers, just align them vertically, and add each column from right to left, just as we do in decimal addition. Remember to carry over any carry digits to the next column if the sum exceeds 1. You can also use a binary addition calculator for quick calculation.

Before that, keep the below rules for addition in mind,

0+0 = 0

0+1 = 1

1+0 = 1

1+1 = 10 (where 1 will be carried over so it will be 0)

For instance, let's add the binary numbers 1010 and 1001

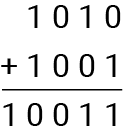
The result is 10011 in binary.

Binary Subtraction:

Suppose you want to subtract one binary number from another. Please do the same as we do in decimal subtraction. Start from the rightmost column and subtract the digits accordingly. Borrow from the next column if necessary. You can also use a binary subtraction calculator.

Before that keep the rules for subtraction in mind,

0-0 = 0

0-1 = 1 (Borrow 1)

1-1 = 0

1-0 = 1

For example, let's subtract the binary number 01100 from 10011:

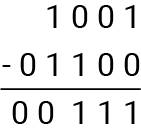
The result is 00111 in binary.

Binary Multiplication:

If you want to multiply one binary number with another, just follow the same principles as we do in decimal multiplication. However, it is only possible with 2 digits. You need to multiply each digit of the second number by each digit of the first number and then add the partial products. You can also use a binary multiplication calculator.

Before that keep the rule for multiplication in mind,

0 x 0 = 0

0 x 1 = 0

1 x 0 = 0

1 x 1 = 1

For example, let's multiply the binary numbers 0100 by 0011:

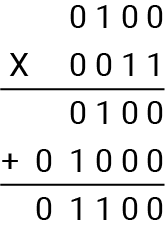
The result is 01100 in binary.

Binary Division:

Suppose you want to divide one binary number with another binary number. You will have to repeatedly subtract the divisor from the dividend while keeping track of the quotient and remainder. The process continues until the dividend becomes smaller than the divisor. You can also use a binary division calculator.

For example, let's divide the binary number 101010 by 110:

The quotient is 0111, and the remainder is 0.