About Our Matrix Multiplication Calculator
What is the Matrix?
In mathematics, a matrix (plural matrices) is a rectangular array or table (see irregular matrix) of numbers, symbols, or expressions, arranged in rows and columns. For example, the dimension of the matrix below is 2 × 3 (read "two by three"), because there are two rows and three columns:
What is Vector?
A quantity having direction, magnitude, especially as determining the position of one point in space that is relative to another.
What is the Difference Between a Matrix and a Vector?
A vector is a list of numbers (can be in a row or column), and A matrix is an array of numbers (one or more rows, one or more columns).
In mathematics and physics, a vector is an element of a vector space. For many specific vector spaces, the vectors have received specific names. Historically, vectors were introduced in geometry and physics before the formalization of the concept of vector space.
What is Matrix-vector Multiplication?
Jacques Philippe Marie Binet is the inventor of Matrix Multiplication who was also recognized as the first to derive the rule for multiplying matrices in the year 1812.
Since we view vectors as column matrices, the matrix-vector product is simply a special case of the matrix-matrix product (i.e., a product between two matrices). Just like for the matrix-vector product, the product AB between matrices A and B is defined only if the number of columns in A equals the number of rows in B.
When we multiply a matrix by a vector, the result is another vector. If our vectors are two-dimensional, we can gain a graphical understanding of the relationship between the input vector and the output vector. It is demonstrated by the following applet. The solid arrows represent the input vectors.
Matrix Multiplication Calculator
A matrix determinant calculator or matrix multiplication calculator is an online tool that assists you in calculating the Matrix-Vector by simply entering the values into the calculator and it automatically gives you the results in a fraction of a second by saving you valuable time without having to calculate the same manually or so.
Complete your super lengthy calculations in just seconds with this matrix calculator.
Graphic Uses of Vector Matrix Mathematics.
Graphic software uses Vector Matrix mathematics to process linear transformations to render images. A square matrix, one with exactly as many rows as columns (Vector), can represent a linear transformation of a geometric object. For example, in the Cartesian X-Y plane, the matrix 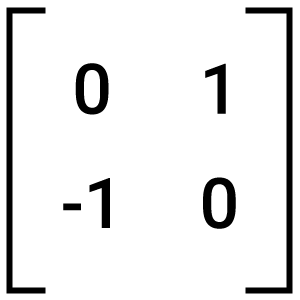 reflects an object in the vertical Y axis. In a video game, this would render the upside-down mirror image of a castle reflected in a lake.
reflects an object in the vertical Y axis. In a video game, this would render the upside-down mirror image of a castle reflected in a lake.
If the video game has curved reflecting surfaces, such as a shiny silver goblet, the linear transformation matrix would be more complicated, to stretch or shrink the reflection
Where Can the Matrix Multiplication Calculator Be Used?
Matrix Vector Calculation can be applied in the study of electrical circuits, quantum mechanics and optics. It is also used in Robotics and automation. Matrices and inverse matrices are also used by programmers for coding as well as for encrypting purposes.
Matrix Vector mathematics has many applications. Mathematicians, scientists and engineers represent groups of equations as matrices; then they have a systematic way of doing the math. Computers have embedded Matrix Vector arithmetic in graphic processing algorithms, especially to render reflection and refraction. Some properties of Matrix-Vector mathematics are important in math theory as well.
Why Matrix-vector Multiplication is Important and Its Relevance?
Matrix-Vector multiplication plays a very important role in many scientific disciplines because of the fact that it is considered the main tool for many other computations in different areas, like those in seismic analysis, different simulations (like galactic simulations), aerodynamic computations, signal and images processing.
In order to do addition, subtraction, multiplication, and many more we’ve created a matrix addition calculator, matrix subtraction calculator, and matrix multiplication calculator. So, leave all your worries on our tool.

 reflects an object in the vertical Y axis. In a video game, this would render the upside-down mirror image of a castle reflected in a lake.
reflects an object in the vertical Y axis. In a video game, this would render the upside-down mirror image of a castle reflected in a lake.