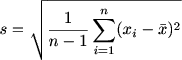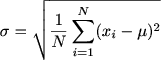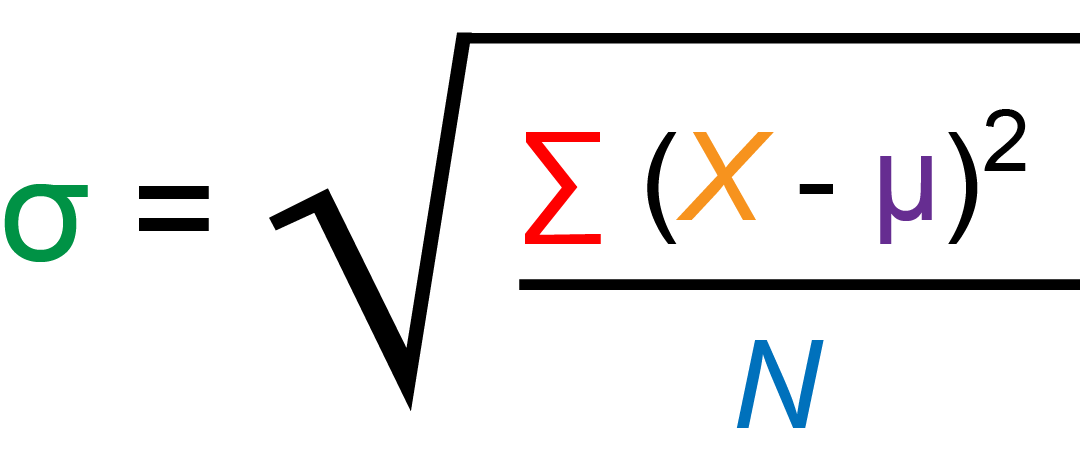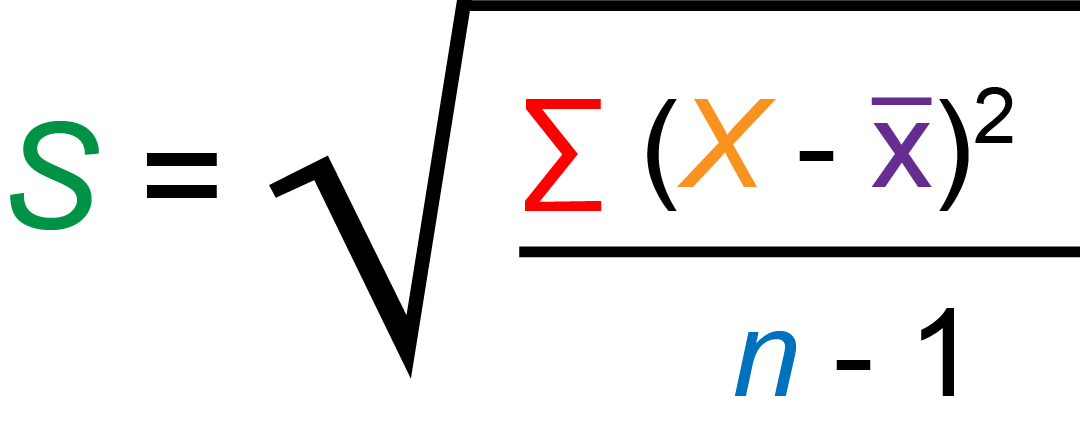About Our Standard Deviation Calculator
The standard Deviation Calculator is very hard to calculate, and in the real world, you can not calculate the standard deviation by hand. That's why the deviation calculator comes into existence. In this article, we will see how to calculate standard deviation with our magical standard deviation calculator.
Standard deviation means the square root of the variance. In your dataset, the standard deviation represents the average variability level; generally, it is "The square root of the variance."
What is a Standard Deviation Calculator?
Online tools like the Standard Deviation Calculator allow users to determine the difference between data sets from the mean.
Standard deviation formulas
The given two formulas are mainly used to calculate the standard deviation.
| Formula - 1 |
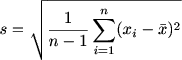
|
S = Sample Deviation,
N = Number of data points,
∑ = Sum,
xi = Individual value,
x̄ = Sample mean
|
Here, n is the sample size, and X- bar is the sample mean.
Here, the second formula for the standard deviation of the whole population Is:
| Formula - 2 |
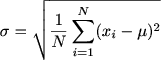
|
σ = Population Standard Deviation,
N = The Size of the Population,
xi = Each Value From the Population,
μ = The Population Mean
|
How to Find Standard Deviation?
The given steps below describe how to calculate the standard deviation. The described steps make your calculation easy and understandable.
- You can use a sample or a population set.
- Divide the result of the Sum of the data values by the number of data values to obtain the mean of the data.
- Divide each data value by the mean.
- Sum up all values after squaring the result.
- To get the standard deviation, divide the Sum of the values by the number of values.
Standard Deviation Formulas for Populations and Samples.
There are mainly two types of the formula used to calculate the standard deviation.
- Population standard deviation
- Sample standard deviation
Population Standard Deviation:
You can calculate the population standard deviation after collecting data from all the members of the population that you want to study.
| Population Standard Deviation |
|
σ = population standard deviation
∑ = sum of…
X = each value
μ = population mean
N = number of values in the population
|
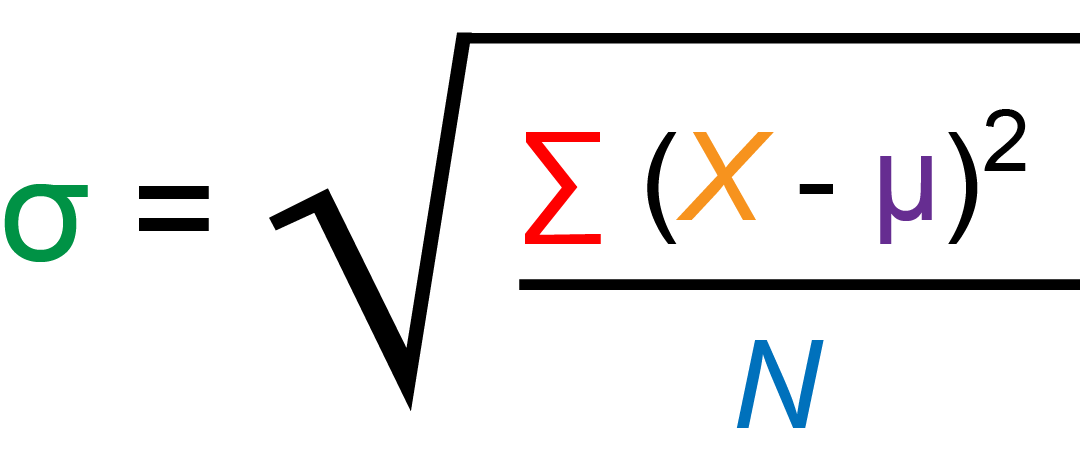
|
Sample Standard Deviation:
One can infer the population's standard deviation using the sample standard deviation in analyzing data from a sample.
| Sample Standard Deviation |
|
s = sample standard deviation
∑ = sum of…
X = each value
x̅ = sample mean
n = number of values in the sample
|
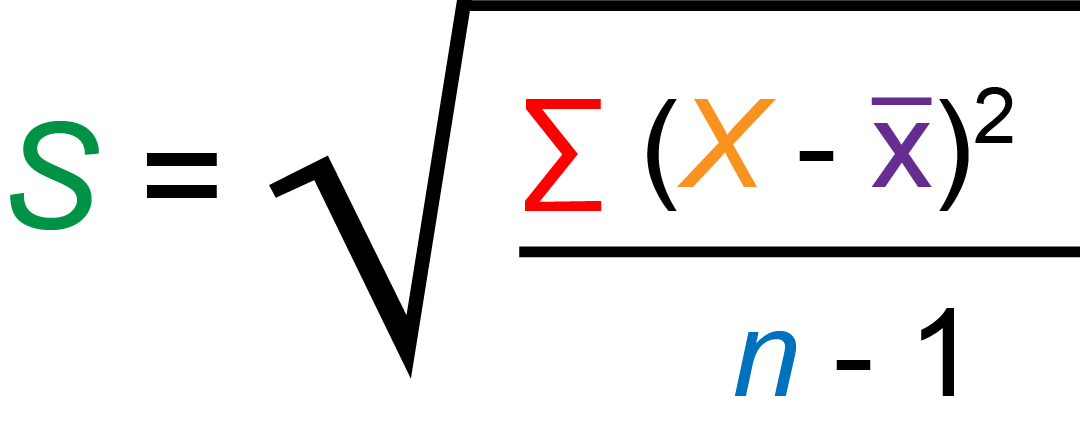
|
Calculate standard deviation with this sample standard deviation calculator.
How Does Standard Deviation Calculator Work?
Standard deviation is regularly signified as SD or σ, giving a proportion of how much an information point has veered off from the mean worth. The mean worth or normal of the given information is characterized by all perceptions separated by the total number of perceptions. A low standard deviation lets us know that the information point is nearer to the mean. Essentially, an exclusive requirement deviation lets us know that the information point is more fanned out than the mean. Below are the means to work out the standard deviation of a given informational collection.
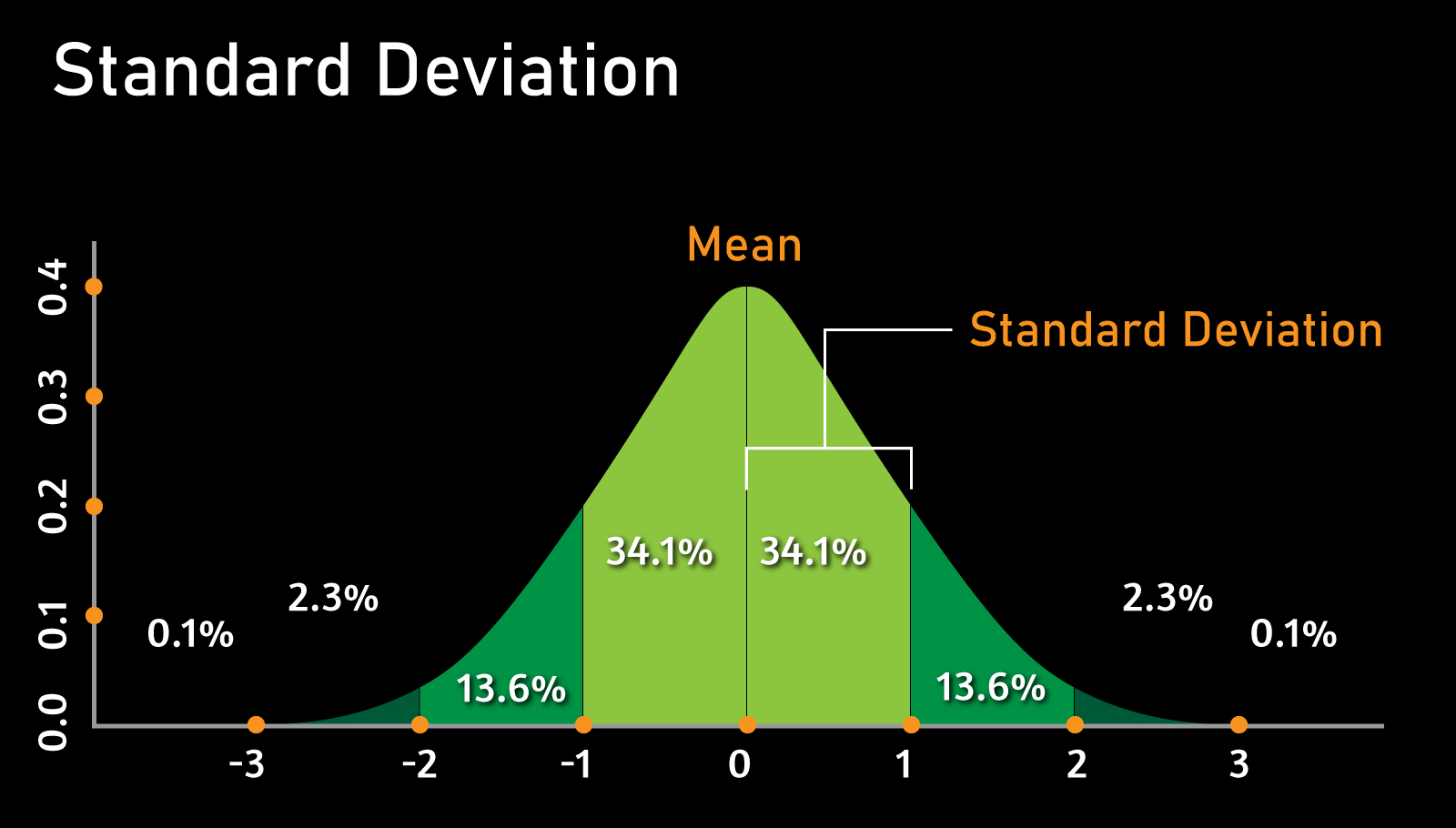
-
Decide the mean of the given worth.
The mean is determined utilising the equation:
Mean or Average(x) = (x1x1+ x2x2 + x3x3...+ xNxN) / N,
where n = total number of terms, x1x1, x2x2, x3x3,
,xNxN = Different N terms.
- Each point in the data set is then subtracted from the mean.
- The values obtained in step 2 are squared, added, and divided by (N - 1). Here N is the number of terms total.
- Finally, the square root of the value obtained in step 4 is determined.
How to Use a Standard Deviation Calculator?
You can use a standard deviation calculator in just a few easy steps.
- Step 1: Open the Standard Deviation Calculator.
- Step 2: Enter the numbers.
- Step 3: Select population or sample.
- Step 4: Click the "Calculate" to get your answer.
- Step 5: Click the "Reset" button to clear out the previous data.
- Step 6: Click the "History" button to check your previous data.
Example: Find out the deviation 4, 9, 11, 12
Mean = (4 + 9 + 11 + 12) / 4 = 9
σ = √[((4-9)2 + (9-9)2 + (11-9)2 + (12-9)2) / 4]
= √[(25 + 0 + 4 + 9) / 4]
= √[38/4] = √9.5
= 3.082